SOBRE LA HISTORIA DE LAS PARALELAS
Breve noticia y comentario
§ 1. El postulado de Euclides y su equivalente: el postulado de la semejanza. "Si una recta que corta a otras dos forma con ellas y hacia el mismo lado dos ángulos internos cuya suma es menor que dos rectos, las dos rectas se encuentran en su prolongación del lado en que la suma es menor que dos rectos". Tal es (en versión del Prof. Francisco Vera) el famoso postulado V de Euclides, que tanto ha dado que hacer a geómetras y filósofos desde hace más de veinte siglos.
Esta proposición nunca parece haber tenido, ni aun para el mismo Euclides, ese carácter de evidencia inmediata y de premisa irreductible que se demanda de un axioma, en el sentido clásico de esta palabra. Lo primero que sorprendió fue tal vez su complejidad. De ahí el recurso de Posidonio (unos 100 años a. de C.): llamar paralelas, no como Euclides, más prudente, a dos rectas que dadas en un plano no se cortan, sino, resueltamente, a dos rectas equidistantes. Bajo el disfraz de una definición lo que así se postula es la existencia de rectas equidistantes. En seguida será muy sencillo demostrar el postulado V... Pero he aquí que el postulado V es, a su vez, la premisa perfecta para demostrar esa equidistancia.
Proclo (410 - 485) que nos da esta noticia, acude por su parte a un recurso sin duda menos candoroso que el de Posidonio, pero no más feliz. Supóngase dos rectas $AB$ y $CD$ que no se cortan.
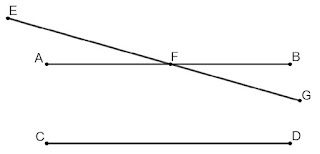
Puesto que la distancia entre ellas es finita, una tercera recta $EG$ que corte en $F$ a la primera, tendrá que cortar a la segunda, ya que un punto móvil sobre el rayo $FG$, se alejará indefinidamente de $FB$ a medida que se aleje de $F$.
Demostrado así el postulado V de Euclides, podrá en seguida demostrarse que la distancia antes propuesta como finita es, además, constante... Es sólo un rodeo para tomar descuidado al toro. Pero no hay que negar por esto su valor. Tales rodeos son los que a la larga han servido para hacer cada vez más transparente la significación del problema, y más inequívoco su planteamiento. Se trata de una larga historia, de una tenaz batalla sin estruendo, pero no por eso menos dramática o imponente que otras más ostensibles. No intentamos hacer aquí ni aun el esquema de esa historia, sino indicar sólo algunos de sus pasos, los más decisivos y, al mismo tiempo, en más directa relación con el norte y estilo de este ensayo.
Es ante todo inexcusable referirse al filósofo y geómetra inglés John Wallis (1616 - 1703), a quien se debe el único postulado que puede competir en diafanidad noética con el postulado V de Euclides: "De toda figura existe siempre una semejante a ella de magnitud arbitraria". Es el llamado postulado de la semejanza. Leibniz (1646 - 1716) nos dirá que si descontada la diferencia de extensión, así como la diversa posición, no se discierne diferencia entre dos figuras, es que son semejantes, que tienen igual forma. (Y ya sabemos que en Leibniz lo discernible no se limita a ser lo distinguible empíricamente). Laplace (1749 - 1827) y Lazare Carnot (1753 - 1823) sustentarán siglo y medio más tarde el mismo supuesto: que el concepto de semejanza, para Carnot tan inmediato, aproximadamente, como el de congruencia o igualdad, no sólo sirve para demostrar el postulado V, sino que le aventaja en sencillez, en naturalidad apriorística, en valor axiomático.
He aquí brevemente el razonamiento de Wallis para demostrar el postulado V de Euclides a partir de la noción común de semejanza:
Sean $A$ y $B$ los ángulos internos formados respectivamente por dos rectas, $R_{1}$ y $R_{2}$, a un mismo lado de una secante común , y cuya suma suponemos inferior a dos rectos.
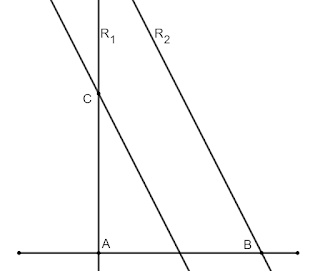
Si mediante la traslación de $R_{2}$ disminuímos de un modo continuo la distancia $BA$ (sin variar el ángulo de $R_{2}$ con la recta $AB$), antes de que esa distancia se reduzca a cero, $R_{2}$ tendrá que cortar a $R_{1}$ en algún punto $C$, determinando con la secante común, $AB$, un triángulo. Si luego acrecentamos de nuevo esa distancia (siempre sin variar los ángulos $A$ y $B$), crecerá la magnitud del triángulo, pero cualquiera que sea esa magnitud se mantendrá su semejanza con el inicial, y por lo tanto permanecerá invariable el tercer ángulo. $R_{1}$ y $R_{2}$ no podrán pues dejar de cortarse, cualquiera que sea la distancia $AB$.
Ahora bien, a partir del postulado V de Euclides se demuestra que la suma de los ángulos de un triángulo plano es siempre dos rectos. Es claro, pues, que si dos de los ángulos permanecen invariables, tendrá que permanecer invariable el tercer ángulo. Es decir, del postulado V se infiere la existencia de triángulos semejantes, y de ésta la existencia, en general, de figuras semejantes. Se demuestra, en suma, la misma premisa que Wallis utiliza para demostrar la proposición euclídea.
§ 2. El método de Saccheri y las geometrías no euclidianas. En la primera mitad del siglo XVIII, un genial italiano, el padre Giovanni Gerolamo Saccheri (1667 - 1733), hace el primer intento de demostración sistemática, continuando la tradición del problema, pero con nuevas y coherentes previsiones metódicas para resolverlo, en su famosa obra Euclides ab omni naevo vindicatus..., publicada en Milán en 1733. Dada la mutua dependencia entre el postulado V y la proposición 32 de los Elementos (según la cual la suma de los ángulos interiores de un triángulo es dos rectos), Saccheri intenta demostrar esa proposición por reducción al absurdo.
La figura fundamental de Saccheri es un cuadrilátero $ABDC$, rectángulo en $C$ y $D$, y de lados $AC$ y $BD$ congruentes entre sí (birrectángulo isósceles), respecto a cuyos ángulos $A$ y $B$ (iguales)

cabe hacer tres hipótesis, que él designa respectivamente como hipótesis del ángulo recto ($A=B= 1$ ángulo recto); del ángulo obtuso ($A=B$ > $1$ ángulo recto), y del ángulo agudo ($A=B$ < $1$ ángulo recto).
Saccheri prueba satisfactoriamente que la segunda hipótesis, la del ángulo obtuso, que implica para todo triángulo una suma angular superior a dos rectos, no es compatible con la potencial infinitud de la recta (postulado II de Euclides); o lo que es igual, se apoya implícitamente en este postulado, como más tarde Lambert, Legendre, Lobachevski..., para excluir del plano dicha hipótesis. Prueba asimismo que la tercera hipótesis (que implica para todo triángulo una suma angular inferior a dos rectos) conduce a la admisión de rectas asintóticas, es decir, de rectas que se aproximarían entre sí indefinidamente sin llegar a encontrarse. Y finalmente sustituye de hecho el postulado V por otro que se podría formular así: Si la distancia entre dos rectas disminuye de un modo continuo, esas dos rectas tienen que encontrarse. O en otros términos: No existen rectas asintóticas. Admitido ese postulado, y asimismo el postulado II de Euclides, ya sólo cabe admitir (hip. del ángulo recto), que todo cuadrilátero birrectángulo isósceles es cuadrirrectángulo. De acuerdo con la proposición 32 de Euclides, la suma de los ángulos de un triángulo es entonces dos rectos y, consecuentemente, se cumple el postulado de la semejanza o, lo que es igual, se cumple el postulado V de Euclides.
Análogo al de Saccheri es el método de otro gran geómetra, el suizo Lambert (1728 - 1777). Parte éste de un cuadrilátero trirrectángulo. Hace sobre el cuarto ángulo las tres inevitables hipótesis (que sea recto, obtuso o agudo), y excluída la segunda, pone de manifiesto que admitir la tercera es admitir la medida absoluta de segmentos (en conexión con la medida absoluta de ángulos). Por distinto camino habría de llegar más tarde el tenacísimo y clarísimo Legendre (1752 - 1833) al mismo resultado. Podría formularse así el "postulado" de Legendre: La magnitud de un segmento no puede ser función directa del valor de un ángulo.
Schweikart y Taurinus, contemporáneos de Gauss, suelen reivindicarse como inmediatos precursores de la geometría no euclídea. Pero esto no impide reconocer en Saccheri al más preclaro precursor... involuntario. Con su modo de plantear el problema del paralelismo Saccheri se sitúa de hecho en el origen mismo de las geometrías no euclidianas, en cuanto éstas no hacen sino llevar más adelante la actitud lógica—o si se quiere epistemológica—implícita en la gran tentativa de Saccheri de demostrar por reducción al absurdo el postulado V. Las consecuencias de excluirlo—piensa Saccheri—deben manifestarse como contradictorias. ¿No son contradictorias? Es decir, ¿puede construirse una teoría coherente—no contradictoria—del espacio a partir de su exclusión? Entonces...
Limitémonos por ahora a hacer historia. Sabemos ya que Saccheri no cree compatible con la naturaleza misma de la recta y del plano (se entiende naturaleza geométrica) la existencia de rectas asintóticas. ¿Por qué? Es para él mismo como un misterio claro y desesperante del que no puede dar razón, y que le hace enmudecer de reverencia, aunque quisiera hablar, argumentar. Y he aquí que esas mismas rectas asintóticas—su admisión hipotética—son las que orientan hasta el fin (o por lo menos hasta el fin de su construcción) a un gran geómetra, el ruso Lobachevski (1793 - 1856), para probar que, excluído del plano, el postulado V se cumple en otra superficie, la horisfera... Superficie teórica, pero no más ni menos teórica (entiéndase hipotética o "puramente racional") que el plano euclídeo. Terrible polvorín de cuestiones, vitales (o mortales) para la mente humana, que dejarían en desorden y sin posible conclusión esta Breve noticia, si cometiésemos la inocente imprudencia de tocarlas aquí.
§ 3. La geometría lobachevskiana (o de Gauss-Lobachevski-Bolyai). El siguiente teorema de Lobachevski, con antecedentes en Legendre, nos permitirá ver en seguida, sin vaguedad alguna, todo el alcance de la exclusión del postulado V en la dirección de esta hipótesis: que la suma angular de un triángulo sea inferior a dos rectos (hipótesis de Saccheri del ángulo agudo).
TEOREMA. Una recta que corta perpendicularmente a uno de los lados de un ángulo agudo (cualquiera que éste sea), no cortará al otro si la distancia entre el pie de la perpendicular y el vértice del ángulo es suficientemente grande.
Sea en efecto $CAB$ cualquier ángulo agudo, correspondiente a un triángulo $CAB$, rectángulo en $B$. Si la deficiencia angular de este triángulo (lo que falta a la suma de sus ángulos para valer dos rectos) es $a$, para su duplicación es, el isósceles $CAD$, será de $2a$.Levantemos en $D$ a la recta $AD$, una perpendicular, y sea $E$ el punto en que encuentra a la prolongación de $AC$.
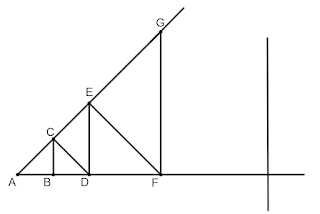
Si la deficiencia correspondiente al triángulo $CDE$ es $z$, la del triángulo rectángulo $ADE$ será $2a+z$. Doble deficiencia corresponderá a su duplicación, el isósceles $AEF$. Así pues, la de un nuevo triángulo $GAF$, rectángulo en $F$, y cuyo vértice $G$ sea un punto de la prolongación de $AE$, será $4a+2z+z^{\prime}$ (si llamamos $z^{\prime}$ a la del triángulo $EFG$). Continuando pues el mismo proceso constructivo, y prescindiendo de los valores indicados con $z$, $z^{\prime}, z^{\prime \prime}$..., tendremos, no obstante ese descuento, una suma angular que crece según la progresión $2a$, $4a$, $8a$, ..., $2^{n}a$. Pero siendo común a todos los triángulos rectángulos así construidos el ángulo invariable $CAB$, el decrecimiento sólo puede afectar al otro agudo, el cual disminuido en $2^{n}a$ sería finalmente, para $n$ bastante grande, un ángulo cero o negativo. No siendo esto posible, alguna de las perpendiculares sucesivas que levantemos en la prolongación de $AB$ no debe ya cortar a la prolongación de $AC$.
Un corolario inmediato es que la perpendicular a la bisectriz de un ángulo, cualquiera que éste sea, puede no cortar a los lados si la distancia entre el pie de la perpendicular y el vértice del ángulo es suficientemente grande. Se sigue, pues, fácilmente, que tres o más tangentes a una circunferencia pueden no cortarse si el radio de tal circunferencia es suficientemente grande, que existen en un plano tantos semiplanos no interferentes como se quiera, etc. De nada vale escandalizarse con los corolarios, ni es lógicamente la actitud más fértil buscar salida a través de su pujante multiplicación.
En la siguiente serie de proposiciones capitales (y aún prescindiendo ahora de su demostración) se advertirá en seguida el potente equilibrio lógico, e incluso arquitéctonico de la concepción lobachevskiana.
1) Sean $C$, $B$, $D$ ($B$ entre $C$ y $D$) tres puntos arbitrarios de una recta $CD$; y $AB$ un segmento perpendicular a $CD$ en el punto $B$. Si $BAL$ es el menor ángulo que puede formar con $BA$ una recta $AL$ que no corte a $CD$, decimos que $AL$ es la paralela a $CD$ por el punto $A$ en el sentido $AL$
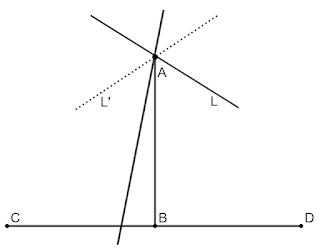
(o en sentido $BD$ si suponemos a un mismo lado de $AB$ los ángulos $ABD$ y $BAL$). Pues bien, en la geometría de Lobachevski el ángulo $BAL$—ángulo de paralelismo—es siempre agudo (ya que si en algún caso fuese recto, sería siempre recto, y se cumpliría el postulado V de Euclides); y tanto más agudo cuanto mayor sea la distancia $AB$. Más aún; del teorema precedente se infiere que ese ángulo podrá ser tan pequeño como se quiera si la distancia $AB$ es suficientemente grande.
2) Nótese que si $AL$ es la paralela a $CD$ por el punto $A$ en sentido $AL$, supuesto el ángulo $BAL^{\prime}$ simétrico del $BAL$ respecto al lado común $AB$, tendremos por $A$ una segunda paralela a $CD$ en sentido $AL^{\prime}$ (o lo que es igual en sentido $DC$ o $BC$). Todas las rectas del plano común a $CD$ y $A$ que pasan por $A$, se dividen pues en dos clases: secantes de $CD$ (las comprendidas en el ángulo $LAL^{\prime}$, con exclusión de las rectas $L$ y $L^{\prime}$); y no secantes de $CD$ (todas las demás rectas que pasan por $A$, entre las cuales se incluyen, naturalmente, las dos paralelas, $L$ y $L^{\prime}$, a la recta $CD$ por el punto $A$).
3) Si $AL$ es paralela a $CD$ por el punto $A$ y en sentido $AL$, en tal sentido la distancia entre ambas rectas decrece continua e indefinidamente sin otro límite inaccesible que cero; y crece en cambio continua e indefinidamente en sentido opuesto. (De acuerdo, pues, con Saccheri, las rectas $AL$ y $CD$ son—o serían—asintóticas. En la terminología de Bolyai, $AL$ es asíntota de $CD$, y $CD$ lo es de $AL$; ambas rectas son paralelas asintóticas.)
4) Dos rectas $h$ y $f$, perpendiculares a una tercera, divergen a partir de ésta, en ambos sentidos, continua e ilimitadamente.
5) Toda línea equidistante de una recta en el plano es una curva (hiperciclo) que opone a la recta su concavidad, y cuya curvatura es tanto mayor cuanto mayor sea el parámetro del hiperciclo: su distancia a la recta.
6) El límite de las circunferencias no es la recta, ni puede serlo un hiperciclo, sino una curva límite (horiciclo) de ejes asintóticos (o según la terminología de Lobachevski, paralelos).
7) A ese orden de líneas corresponde un orden de superficies. El hiperciclo es la recta de una hiperesfera (superficie equidistante de un plano). El horiciclo es la recta de la horisfera, límite de una esfera de radio creciente y de una hiperesfera de parámetro creciente.
8) En una hiperesfera, la suma de los ángulos de un triángulo es, como en el plano, menor que dos rectos. Para triángulos de extensión constante, tal suma se aproximará tanto más a dos rectos cuanto mayor sea el parámetro de la hiperesfera (es decir, su distancia al plano del cual equidista). En la horisfera el déficit se anula. Al pasar a la esfera nos hallamos con la inversión del signo. El déficit, a través de cero, pasa a ser exceso, tanto menor, como es sabido (siempre para triángulos de la misma extensión), cuanto mayor sea el radio de la esfera.
9) Puesto que en la horisfera la suma de los ángulos de un triángulo es dos rectos, en ella se cumple el postulado de Euclides, y el postulado de Wallis: allí sí, habrá triángulos semejantes.
Aunque tal concepción se ha consagrado con el nombre de "lobachevskiana", todos los buenos estudiantes de historia de la geometría saben la gloria que en el proceso o culminación de tan extraordinario descubrimiento lógico cabe principalmente a Gauss, "príncipe de los matemáticos" (1777 - 1855), y al húngaro, oficial del ejército austríaco, János Bolyai (1802 - 1860), hijo y discípulo de otro gran geómetra (Farkas Bolyai) que no pudo apartarle de tan aventuradas investigaciones, si bien fue luego, al ver el fruto, el primero en celebrarlas: ... "Si la cosa está realmente conseguida, conviene darla a la luz pública: primero, porque las ideas pasan fácilmente de uno a otro, que acaso se anticipe a publicarlas, y luego porque hay también mucho de verdad en esto: que muchas cosas tienen una época en la cual son descubiertas a la vez en varios lugares, de igual modo que por la primavera brotan las violetas en todas partes"...
§ 4. Riemann, o la exclusión del paralelismo. Tres hipótesis: tres geometrías. En todas las investigaciones aludidas se había dado siempre por supuesta la no finitud de la recta (o sea, según el postulado II de Euclides, la posibilidad de prolongar ilimitadamente una recta limitada, un segmento de recta). Se partía asimismo (lo uno implica lo otro) de la existencia en el plano de rectas no secantes, ya en cierto modo postulada por Euclides en su definición de paralelas: "rectas de un plano (entiéndase segmentos) que prolongadas por sus dos partes, en ninguna se encuentran".
Riemann (1826 - 1866) es el primero en excluir la existencia en el plano de tales rectas no secantes, al adoptar con todas sus consecuencias la hipótesis del ángulo obtuso, de Saccheri. En su geometría no hay rectas paralelas, ni euclídeas ni lobachevskianas. La recta es cerrada (se excluye así el postulado II); y hay en el plano pares excepcionales de puntos, análogos a los diametralmente opuestos de una esfera, por los cuales no pasa una sola recta (no determinan una recta), sino infinitas rectas.
Llamemos $S$ a la suma de los ángulos de un triángulo. Las tres hipótesis respecto a esa suma se corresponden con tres geometrías: de Euclides ($S=2$ ángulos rectos); de Gauss-Lobachevski-Bolyai ($S$ < $2$ ángulos rectos), y plano esférica de Riemman ($S$ > $2$ ángulos rectos).
Dada la conexión entre las tres hipótesis sobre la suma de los ángulos de un triángulo y las que pueden proponerse a priori sobre el paralelismo, la anterior distinción puede también establecerse así:
I) Si $A$ es en un plano un punto exterior a una recta $\ell$, por ese punto se puede siempre trazar una recta, y una sola, que no encuentre a $\ell$ (Euclides).
II) Se pueden trazar por $A$ infinitas rectas no secantes de $\ell$ (Lobachevski).
III) Por el punto $A$ no pasa recta alguna que no corte a $\ell$ (Riemann).
De más esta decir que adoptar una de las tres hipótesis no es hacerse adversario del que adopte alguna de las otras dos. En el siglo pasado aún se admitía la posibilidad de la comprobación empírica (midiendo los ángulos de un triángulo suficientemente grande). Razones no sólo prácticas, sino epistemológicas, han ido haciendo declinar la fe en ese recurso. Entretanto sabemos que la tercera hipótesis no es hipótesis, sino un hecho cierto y "euclidiano", si la referimos a la superficie esférica, y que asimismo la segunda (dentro de ciertos límites, o sea prescindiendo de aquellos corolarios que sólo tendrían sentido en el plano) se cumple en superficies de curvatura negativa. Así entendidas, no hay gran razón para inquietarse...
§ 5. Comentario. Y sin embargo, la inquietud subsiste. Se sabe muy bien que no se trata de la esfera ni de la seudoesfera, sino del plano, y que es justamente por ser inequívocamente plano el plano por lo que puede alguna vez tener sentido este fértil convenio: llamar plano al espacio, por ejemplo... Se sabe asimismo, más o menos de soslayo, que no hay digno sosiego para la mente si Dianoia y Noesis se mueven guerra en ella, y más aún si es guerra fría, como ahora se dice.
Se construyen modelos tangibles y modelos simbólicos, acompañados de diccionarios para la justa interpretación de las líneas y de sus relaciones, que muestran la conciliación teórica de las tres geometrías, mientras nos mantengamos, diplomáticamente, al margen de la llamada representación intuitiva del plano. Representación intuitiva... No es fácil saber de que se trata, al menos si se sobrentiende que es algo "inferior" y, en cierto modo, hostil a la representación discursiva del mismo plano, es decir, del mismo plano al cual se refiere el discurso. Ciertamente éste, a partir de la crisis de los postulados, puede referirse a tres planos, que se declaran (los tres) hipotéticos y que, en principio, son el mismo plano, ya que él, a ese plano único, se refieren las tres hipótesis que dialécticamente lo diversifican. ¿Cómo puede ser? ¿Es que ese mismo plano se desdice, y la suma angular de sus triángulos es a la vez dos rectos, y mayor o menor que dos rectos? Para la representación intuitiva las consecuencias de suponer que es mayor o menor que dos, entran pronto en discordia con la representación del plano. Fiel (como es lógico) a esa representación inicial, que es además la subsistente, la intuición retrocede, o bien resuelve curvar las rectas elegantemente y sigue adelante, siempre en espera (por exigencias lógicas, de fidelidad a lo previamente dado o mencionado) de que terminen por enderezarse. La epistemología (al menos la vigente) no toma en serio esta esperanza ni aquel retroceso. ¿Cómo se justifica esa indiferencia? Ahí se pasan los límites de la epistemología para entrar en los de un cierto dogmatismo formalista escéptico, que tampoco es seguro que pueda (ni quiera) calificarse de filosofía, y cuyas variantes, escuela y matices no cabe aquí, sin riesgo de injusticia, reducir a esquema. En general se tiende a dar por definitivamente establecido que un postulado o un axioma no es más que una "regla de juego". No tendríamos gran dificultad en concederlo si al decir juego no se entendiese algo movido por la regla, o ya implícito en ella, y sin otro destino que confirmar la interna consecuencia de la regla misma y si, por otra parte, al decir regla se entendiese algo más que convenio previo entre los jugadores. La regla más honda y viva puede ser ignorada, y el que juega de verdad—como un torito en una pradera—no siempre da en creer, por suerte, que eso que hace es puro juego. ¡Si se dijese puro diálogo!...
De un diálogo justamente se trata, se nos dice, un diálogo en el cual, dicha una cosa, ya no hay que desdecirse mientras no se llega al absurdo, el cual sólo consiste en decir lo contrario de lo que se había dicho , y esto como rigurosa consecuencia de lo que se había dicho.
Nada hay que oponer a esto. Es sin duda un gran método (allí donde el sentido de orientación nos haga presentir que es, en efecto, un método) mientras de ahí no se infiera que todo el valor de aquello que se ha empezado por decir reside en la posibilidad de poder seguir diciéndolo indefinidamente. Sin duda eso es parte del valor lógico de una proposición, pero otra parte importante es que sea lógica, lo cual exige que tal proposición no sea soberana de una isla perdida, incomunicada...
¡Todas se comunican! dice de nuevo nuestro interpelante. Y ahí reside exactamente la unidad y hasta la libertad del entendimiento, pues—quiera o no acompañarlo la intuición—puede ir a la isla en que se dice si y (si está bien gobernada) decir si; y luego ir a la isla en que se dice no y decir también no, y esto sin desdecirse, pues lo único que dice es que una isla debe estar bien gobernada. ¿Y el buen gobierno? Simplemente un gobierno consecuente, a partir de convenios bien establecidos, es decir: a partir de axiomas suficientes, compatibles y, a ser posible, no superabundantes. Es ocioso—ingenuo—preguntarse si el plano es plano o esférico. Tan racional es una hipótesis como la otra. Sólo es cuestión de convenir lo uno o lo otro y de formalizar bien el convenio, dándole forma de premisas que nos permitan sustentar sin contradicción lo uno o lo otro. Y como lo uno puede siempre traducirse a lo otro (para eso están los convenios nominales) la no contradicción de lo uno es justamente la garantía de la no contradicción de lo otro...
Aquí aparece algo de auténtico valor: los diccionarios... No, no puede haber inconveniente alguno (es fértil para ciertas investigaciones lógicas, y acaso inexcusable para dar máxima transparencia o agilidad a ciertas disciplinas geométricas) en llamar punto a la recta, recta al plano, plano al espacio..., siempre que no se intente llevar esa transferencia de nombres, y con carácter de criterio, al terreno mismo en que se están queriendo investigar las propiedades irreductiblemente distintivas de lo que se nombra. Y si se dice: No existe lo que se nombra, sino sólo el nombre, se empieza por un postulado asombroso, impropio de la majestuosa modestia de la geometría. Aun cuando sí, podría ser verdad, con un alcance tal vez no deseado por los nominalistas, dándole este otro giro: Lo que se nombra es apenas la sombra del nombre.
***
CRÉDITOS. Encontré este ensayo en el primer capítulo del Nuevo tratado del paralelismo del poeta Rafael Dieste (dicho libro fue publicado en 1956 por la editorial argentina Atlántida). Aunque tengo conflictos con algunos puntos del ensayo, decidí "subirlo" a la bitácora para futuras referencias. Cabe mencionar que fue a través de un artículo que Letras Libres le publicó a Gabriel Zaid que supe de la pasión de Dieste por la geometría; el artículo lleva por título Problemas archivados y se encuentra disponible en este rincón del portal de la revista.





